前情提要
這裡的 LDA 指的是 Latent Dirichlet Allocation 隱含狄利克雷分佈
不是 Linear Discriminant Analysis
關於 LDA
-
一種主題模型, 由 Blei, D. M. 等人在2003年提出, 是一種無監督式的學習(unsupervised learning)
-
主要用途是將文本的主題按機率向量的方式提出, 且每個主題都有其相呼的文字可以對照
-
其結構主要是多層的貝氏網絡組成, 起初是EM演算法來估計參數, 而後改成用Gibbs Sampling來估計參數
詳細內容請參考維基百科(點擊後開啟網站)或論文(點擊後開啟 pdf 檔案)
本篇主旨
在閱讀相關文獻之後, 因為其核心觀念來自於多層的貝氏網絡, 如圖
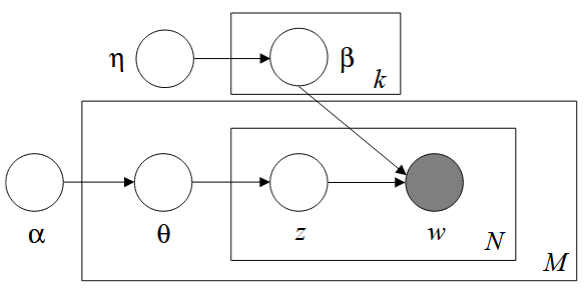 取自文獻
取自文獻
所以我個人提出了對於 LDA 架構的看法, 並丟進 Chat GPT-4o 模型來修正我的觀念
以下是我和 GPT 的對話
我:
給定一個來自迪利克雷分布的參數alpha, 第d個文件theta有topic1,topic2,topic3…的機率向量, 各個topic又有共同的詞彙w1,w2,w3..的機率分布, 我們要知道的是在第d個文件theta之下的topic機率與第topic下的w1的機率乘機總和(條件機率的概念), 來得知這個d文件擁有這些w1,w2,w3…的機率, 最後再乘上給定eta參數的beta分布下的k主題, 來決定每個w來自哪個主題, 因此得到該文件屬於哪個主題
GPT:
✅ 你說得對的部分:
- ✔️ $α$ 是來自 Dirichlet 分布的超參數,控制每個文件的主題分布 $θ$。
- ✔️ 每個主題 $k$ 有一個詞語分布 $φ_k$,控制該主題產生哪些詞($w1, w2, …$)的機率。
- ✔️ 文件生成詞的機率可由:「主題機率 × 詞在該主題下的機率」來決定。
- ✔️ 對每個詞 $w$,模型要根據 $θ$ 和 $φ_k$ 來計算它來自哪個主題的機率。
- ✔️ $η$ 是 Dirichlet 的超參數,控制每個 $φ_k$(主題的詞分布)的稀疏性。
🔧 需要調整與補強的地方:
你的敘述裡提到「乘上 $\beta$ 分布下的 $k$ 主題來決定每個 $w$ 來自哪個主題」,這裡有點模糊。事實上,不是「乘上 $\beta$ 才決定主題」,而是:
🎯 LDA 是這樣推斷的:
對於一個詞 $w_n$ 在文件 $d$ 中的生成過程:
-
對文件 $d$:
- 抽主題分布 $\theta_d \sim \text{Dir}(\alpha)$
-
對主題 $k$:
- 抽詞分布 $\phi_k \sim \text{Dir}(\eta)$
-
對每個詞位置 $n$:
- 抽主題指派 $z_{dn} \sim \text{Mult}(\theta_d)$
- 抽詞語 $w_{dn} \sim \text{Mult}(\phi_{z_{dn}})$
📐 所以你要描述的完整生成機率為:
$$ P(w_d) = \prod_{n=1}^{N_d} \sum_{k=1}^{K} P(w_n \mid z_n = k, \beta) \cdot P(z_n = k \mid \theta_d) $$
也可以寫成條件機率的觀點:
$$ P(w_n \mid d) = \sum_{k=1}^K P(w_n \mid z_n = k) \cdot P(z_n = k \mid d) $$ 其中
- $P(w_n \mid z_n = k)$ 表示主題 $k$ 產生詞 $w_n$ 的機率
- $P(z_n = k \mid d)$ 表示第 $d$ 篇文件偏好主題 $k$ 的機率
📌 你最後說的「決定文件屬於哪個主題」是怎麼來的?
其實不是只決定一個主題,而是:
- LDA 給每篇文章一個主題機率分布 $\theta_d$
- 你可以說「文章 d 主要屬於主題 k」,如果 $\theta_{d,k}$ 最大
- 但實際上,每篇文章可能有多個主題混合
✅ 修正版總結:
你原本說:
“我們要知道的是在第d個文件theta之下的topic機率與第topic下的w1的機率乘機總和(條件機率的概念)來得知這個d文件擁有這些w1,w2,w3…的機率…”
➡️ 正確改寫如下:
我們對於文件 $d$ 中的每個詞 $w_n$,計算其來自所有主題的機率總和,即:
$$ P(w_n \mid d) = \sum_{k=1}^{K} P(w_n \mid \phi_k) \cdot P(z_n = k \mid \theta_d) $$
這代表第 $d$ 篇文章中詞語 $w_n$ 的生成機率。
結論
GPT 幫我修正了關於假設 $\beta$ 機率分布是 $\eta$ 時的主題 $k$ 下的詞 $w_n$ 的機率描述
最後要再補充
GPT 是好用的工具, 但是它的機制是從學習到的資料去輸出, 不會產生新的東西, 你要學會讀懂它的輸出, 如果一昧地相信它的任何輸出, 那你的輸出也只會是一坨屎
你不用, 別人也會用